
Specifying attribute hierarchies
Source:vignettes/articles/attribute-hierarchies.Rmd
attribute-hierarchies.RmdWhen specifying a diagnostic classification model (DCM), it is common to define relationships between the measured attributes. For example, one attribute may be a precursor or successor to another attribute. In other words, the attributes form a hierarchy. In this article, we describe how to define different hierarchical relationships with dcmstan.
Choosing a structural model
dcmstan supports two structural models that have the ability to
specify an attribute hierarchy. The hierarchical diagnostic
classification model (HDCM; Templin & Bradshaw, 2014) can be defined
with hdcm(). The HDCM assumes a strict attribute hierarchy.
That is, possible profiles that conflict with the defined hierarchy are
completely excluded from the model. On the other hand, we can use a
Bayesian Network (BayesNet; Hu & Templin, 2020) as the
structural model using bayesnet(). The BayesNet enforces a
less restrictive hierarchy. All possible profiles are still included in
the model, but profiles that are inconsistent with the defined hierarchy
are less likely.
Both hdcm() and bayesnet() include a
hierarchy argument that can be used to define specific
relationships between attributes. In the following sections, we describe
different attribute structures and show how to define these structures
with dcmstan.
Attribute structures
In general, hierarchies can be classified into two broad categories: simple and complex structures.
Simple structures
For simple structures, attributes can exhibit a linear, converging, or diverging relationship.
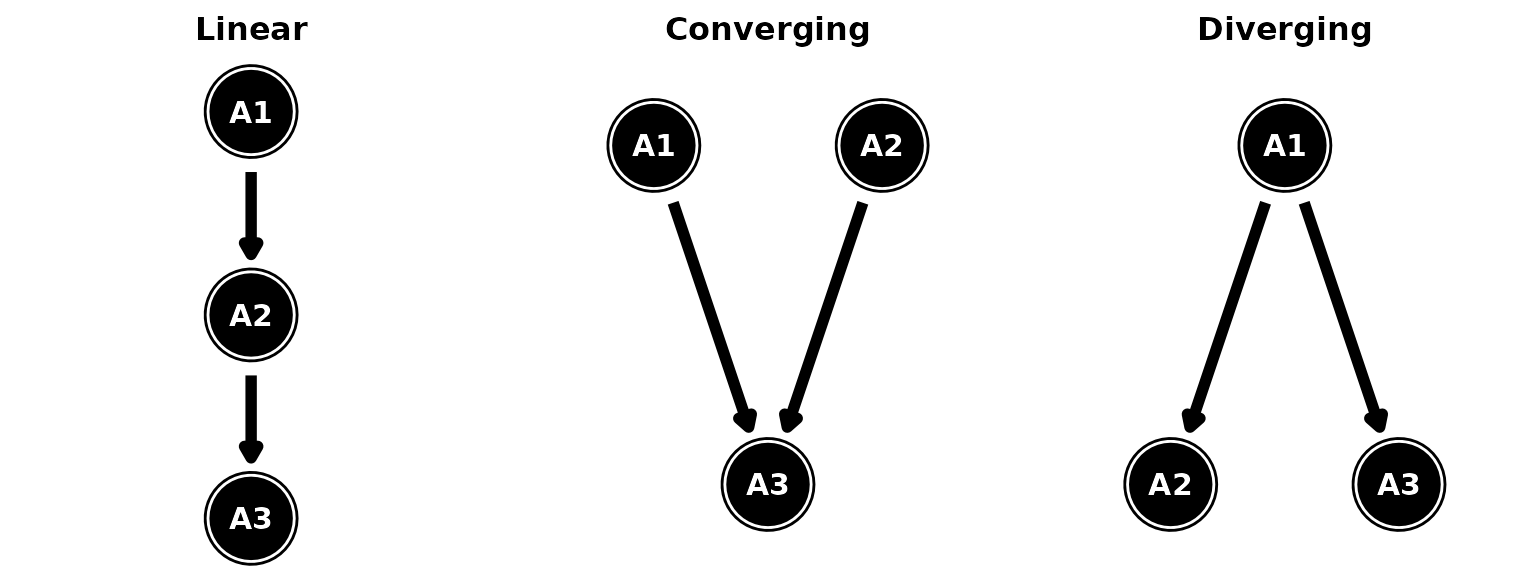
Simple attribute structures
In a linear structure, the attributes must be acquired in a specific order, one after the other. In the figure, a respondent must be proficient on A1 before they can acquire the skills in A2, followed by A3. We can specify this relationship in dcmstan as:
hdcm(hierarchy = "A1 -> A2 -> A3")We use arrows (->) to denote dependencies between the
attributes. In the linear example, we defined the entire hierarchy with
one continuous string of attributes (i.e.,
"A1 -> A2 -> A3"). However, we could also define each
pairwise relationship separately. For example,
"A1 -> A2 A2 -> A3" would be an equivalent
specification. Alternatively, we can also define the hierarchy in a
separate variable that is passed to the structural model function.
Consider a converging structure, where proficiency of two or more
attributes is required before a culminating attribute. All of the
following specifications are equivalent.
hdcm(hierarchy = "A1 -> A3 <- A2")
hdcm(hierarchy = "A1 -> A3 A2 -> A3")
converge <- "
A1 -> A3
A2 -> A3
"
hdcm(hierarchy = converge)Finally, we can similarly define a diverging structure, where one
attribute serves as a precursor to two or more attributes. Note that
although we have used hdcm() in these examples, the same
hierarchy specifications can be provided to bayesnet() as
well.
Complex structures
In a complex structures, multiple simple structures are combined into a larger web of attribute relationships. Depending on the number of attributes included on an assessment, there are an almost unlimited number of structures a hierarchy could take by mixing linear, convergent, and divergent relationships. As an overview of how different structures can be specified in dcmstan, we’ll consider a few example structures with two, three, four-levels of hierarchy.

Complex attribute structures
In the two-level structure, A1 and A2 serve as precursors to two attributes each. A3 and A4 are the culminating attributes of A1, while A4 and A5 are the culminating attributes of A2. A4 represents a converging relationship between A1 and A2. As with the simple structures, this relationship can be specified as one continuous chain or as a series of different relationships. All are equivalent.
hdcm(hierarchy = "A3 <- A1 -> A4 <- A2 -> A5")
hdcm(hierarchy = "A1 -> A3 A2 -> A5 A1 -> A4 <- A2")
complex2 <- "
A1 -> A3
A1 -> A4
A2 -> A4
A2 -> A5
"
hdcm(hierarchy = complex2)Similarly, we can define a three-level hierarchical structure that
mixes linear, converging, and diverging structures. In this
configuration, A1 diverges to A2 and A3. A3 then is a convergence
between A1 and A4. Finally, A5 has a linear dependency on A3. In this
example, the full structure can not be written as a single chain .
Therefore, we can specify the structure in as two smaller relationships,
such as "A2 <- A1 -> A3 <- A4" and
"A3 -> A5", or as a series of pairwise relationships as
in the previous examples.
hdcm(hierarchy = "A2 <- A1 -> A3 <- A4 A3 -> A5")
complex3 <- "
A1 -> A2
A1 -> A3
A4 -> A3
A3 -> A5
"
hdcm(hierarchy = complex3)Finally consider a four-level hierarchy that also mixes all three simple structures, but in different configurations. In this example, A1 is a linear precursor to A2. A2 then diverges into A3 and A4, which both then converge back on A5. This structure again can be defined in a single chain, multiple smaller relationships, or pairwise relationships equivalently.
Disallowed structures
So far, we have discussed how different attribute structures can be specified within dcmstan. However, there are some structures that are not allowed. Namely, a structure must be a directed acyclic graph (DAG; Almond et al., 2015), meaning that if we follow the directions of the arrows, we must not be able to form a closed loop and return to an attribute we have already visited.

Invalid attribute structures
In the first example, we can start at A1 and return to A1 by
following the path A1 -> A2 -> A3 -> A1. Similarly
in the second example, there are multiple closed loops. For example, we
can create a loop from
A1 -> A5 -> A2 -> A4 -> A1 or
A3 -> A4 -> A1 -> A5 -> A2 -> A3. Thus, both
of these structures would be invalid. If you specify and invalid
attribute structure, you will be met with an error.